Some example problems follow
| |
If this is the first time you'll be using the slide rule, please pay very close attention, work slowly,
and please do not allow yourself to feel intimidated by all the tiny lines and numbers. The slide
rule is very simple to use! Once you learn how to do just a few problems, everything will begin to
make sense.
|
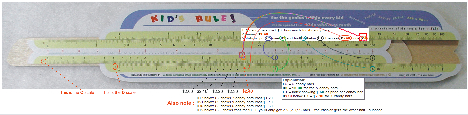
Example slide rule problem #1
*
The example below cannot be used by those participating in the free slide rule giveaway
* Special note: you can use a virtual slide rule to practice on
|
If 5 candy bars cost $3, how much for 4 candy bars?
Answer: $2.40
Solution:
put C5 over D3 and find
D6 below C1, then see D240 under C4
Explanation:
C5 = 5 candy bars
D3 = $3.00 for the 5 candy bars
C1 = index showing $.60 as price per candy bar
D240 below C4 = $2.40 for 4 candy bars
Then without moving the slide:
D12 below C2 shows 2 candy bars cost $1.20
D54 below C9 shows 9 candy bars cost $5.40
D36 below C6 shows 6 candy bars cost $3.60
|
click image below to expand
The example image linked to below is rather large.
You may need to tell your browser to show it full size after it loads.
|
|
D15 below C25 shows that for $1.50 you'll only get 2.5 (2-1/2) bars - the cashier gets the other half I suppose.
What's going on in this problem?
Placing C5 over D3, divides
3 by $5.00. The answer to that
problem, $.60 can then be found below C1. The C1
is often referred to as an index, and is used frequently in problems such as this. After
placing the slide rule in that position, a "table" of relationships of the same ratio is created.
In the example above, we then try to find how much 4 candy bars
would cost, and the only requirement is to simply look under the 4
where we find the value, $2.40.
If you think about what just happened,
you may then realize that to find out a price for any amount of candy bars with this relationship
between price and quantity, all that is required is to look under the quantity to find the price.
Did you notice how simple this type of math is to do on the slide rule? With a hand-held calculator,
this problem would have required a lot of pressing of the buttons to get many answers.
Now, try it on a virtual slide rule
|
Example slide rule problem #2
*
The example below cannot be used by those participating in the free slide rule giveaway
|
You can do addition by multiplying and dividing on the "Kids Rule!" slide rule, but you will need to be able to add 1
to any number in your head for this to work.
The formula is (A/B + 1) x B = answer.
Example:
add:
10 + 5 = 15
mult/div:
(10/5 + 1) x 5 = 15
Solution:
move the slide right, putting C5 over D10 and find
D2 below C1, then add 1 in your head, making the
2 a 3. Move the slider left until
C1 is over D3. Finally, read the answer of
D15 below C5
What's going on in this problem?
Placing C5 over D10, divides
10 by 5. The answer to that
problem, 2 can then be found below C1. As mentioned in
the previous problem, C1 is often referred to as an index, and is used frequently in problems
such as this. Now we have the answer to the first part of the problem. Next we add
the 1 in our head to get 3. The next thing in the formula is to
multiply the 3 by 5, so we place
our index, C1 over D3 and look for the answer below
C5, which turns out to be 15, as promised!
Now, try it on a virtual slide rule
I'll return to this example with pictures of the settings
on the slide rule to perform the task, just as in the first example.
|
Example slide rule problem #3
*
The example below cannot be used by those participating in the free slide rule giveaway
|
You can multiply 3 numbers with a single move of the slide on the "Kids Rule!" slide rule.
The formula is:
1.) CI-1st number to multiply,
goes over top
D-2nd number to multiply.
2.) pick any C-3rd number, and final
answer is below on D.
Example:
multiply:
5 x 3 x 4
= 60
Solution:
move the slide right, putting CI5 over D3, below
C1 you'll see D15 - an intermediate answer. Move the cursor to
C4 and below it find the final answer C60
What's going on in this problem?
Placing CI5 over D3, sets the slide
rule to multiply, using the "inverted" scale. The answer to a multiplication of this form is then found
below C1
Then without moving the slide:
D9 below C6 shows
5 x 3 x 6
= 90
D45 below C3 shows
5 x 3 x 3
= 45
D75 below C5 shows
5 x 3 x 5
= 75
also notice:
D9 below C6 shows
25 x 6 x 6
= 900
D45 below C3 shows
75 x 2 x 3
= 450
D75 below C5 shows
2 x 75 x 5
= 750
Now, try it on a virtual slide rule
I'll return to this example with pictures of the settings
on the slide rule to perform the task, just as in the first example.
|
|
